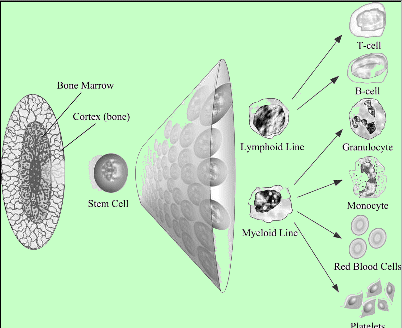What Is Leukemia? Leukaemia comes from a Greek word meaning “white blood” and is often referred to as cancer of the blood. The term refers to a group of closely related malignant conditions affecting the immature blood-forming cells in the bone marrow.so is that certain cells in the body become abnormal. Another is that the body keeps producing large numbers of white cells . Common symptoms of leukemia: Anemia       Fever Weakness and fatigue Frequent infections Loss of appetite and/or weight Swollen or tender lymph nodes, liver, or spleen Easy bleeding or bruising Tiny red spots (called petechiae) under the skin Swollen or bleeding gums females. Sweating, especially at night; and/or Bone or joint pain.

Deaths: Some 21,600 persons will die from leukemia this year in the U.S; approximately 12,000 males and 9,600

Causes of Leukemia

The specific cause of leukemia is still not known. Scientists suspect that viral, genetic, environmental, or immunologic factors may be involved.

Some viruses cause leukemia in animals; but in humans, viruses cause only one rare type of leukemia. Even if a virus is involved, leukemia is not contagious. There is no increased incidence of leukemia among people (friends, family, care givers) who have close contact with leukemia patients.

There may be a genetic predisposition to leukemia. There are rare families where people born with Chromosome damage may have genes that increase their chances of developing leukemia.

Chemicals: The commonest chemical exposure linked to leukaemia is probably cigarette smoking. Benzene in high concentrations is known to cause leukaemia and it is possible that other, similar organic chemicals, may increase the risk of leukaemia and related diseases. 

Radiation: Ionizing radiation is the term used for the kind of radiation given off by X-ray machines or by radioactive materials. High doses of radiation can definitely increase the risk of leukaemia and related diseases. This was shown by the atomic bomb survivors and by the experience of other people accidentally exposed to high levels of radiation.

Methods of Treatment

• chemotherapy antineoplastic (the use of drugs to kill cancer cells): 2'-Deoxy-2-chloroadenosine"; Vincristine, Cyclophosphamide, Cytosine arabinoside. Melphalan etc....
• radiation therapy Radiation therapy, also called Radiotherapy, uses high-energy rays to damage cancer cells and stop them from growing. The radiation comes from a large machine.
• bone marrow transplantation
• biological therapy therapy involves treatment with substances that affect the immune system's response to cancer. Interferon is a form of biological therapy that is used against some types of leukemia.

• BIBLE CODE MATRIX
• Code Matrix Location Genesis 10:29 to Genesis 40:16

  Encoded Words:

  Central Term Leukemia Skip 2075 Cancer    Disease   Blood      Malignant   Evil    Cells  Cell   theWhite     Cause    Existence    Alteration     in theGenes   Virus  Radiation    Bleeding  Anemia    because of that      He did Substance   Chemical    Therapy    2-Chloro Adenosine

Cluster 1 : Row Split by 3

Cluster 2 (The Same Matrix, with more encoded words) Row Split by 3

Cluster 3 : Row Split by 6

Statistical Analysis-Probability of the Matrix

What is the statistical relevance of the Cluster 1, 2, and 3 matrix?  

If we add up the positive matrix R-values from the Cluster 1 Matrix Report, we get a cumulative matrix R-value of ( 9.101 )(using the text R-value for the main term). Then taking the antilog of the total matrix R-value, we get( 1,261,827,534.590670 ). That means that cluster 1 is very relevant when viewed statistically from a frequency point of view. There is 1 chance in 1,261,827,534 of the matrix occurring with all of the terms in such a small matrix. Or as stated in expected occurrence for the matrix, we'd expect 0,00000000792 chance of occurrences. Let's restate it in another way much more conservatively. Cluster 1 has 506 letters,so there are 602.38 matrices of that size in the Torah (304,805 DIVIDED BY 506) ).Conservatively then,if we divide the above chance of occurrence by 602.38 , then we still have a probability of 1 chance in 2,094,736 , or an expected matrix occurence of 0.0000004.

We can also divide it by the row split to account for looking at 1-7. 2,094,736 divided by 3 equals 698,245. Therefore, conservatively stated, the probability of cluster 1 above is 1 chance in 698,245. This is a very significant matrix.

Webmaster note: There is controversy regarding calculating code matrix terms from the surface text as if they were random terms for statistics purposes. We believe that one should note the meaningfulness of surface terms (those at an ELS of +1) in the explanation, but not include them for statistical purposes. When we add up significant terms from cluster 1 (ignoring terms in the surface text at an ELS of +1), we get an overall R-value of 3.022. We then measure the expected occurrences of the main term for an ELS search range of -2075 to 2075 in the Torah and note there are 10.96 expected occurrences. We calculate E=1052, and divided by 10.96 equals 95.98. Next we conservatively correct it for a row-split of 3, by dividing by 3. Our final odds for cluster 1 matrix are 1 chance in 32, or 0.313. This is not a very significant matrix if we conservatively ignore terms from the surface text for statistics purposes.

Webmaster note: Recalculating the statistics and ignoring the terms at an ELS of +1 in the surface text, the overall R-value is 3.753 and E=5662.4. Dividing by the expected occurrences of the main term in the Torah, 10.96, we get 5662.4 divided by 10.96=516.6. Corrected for a row-split of 3 we get odds for the matrix of 1 chance in 172, or 0.00581. While this is higher than cluster 1, it still is not a very significant matrix, when the terms from the surface text at an ELS of +1 are ignored for statistics purposes.

Webmaster note: Ignoring terms from the surface text at an ELS of +1 for statistics purposes, the overall R-value is 5.651. Corrected for 10.96 expected occurrences of the main term in the Torah, and a row-split of 6, we get odds of 1 chance in 6808 or 0.000147. This is more significant than cluster 1 & 2, but not as significant as other matrixes on this site. I would still term it a minor matrix.